RQES2020Sで発表予定だった「非線形成分を考慮したMT法（2次元非線形MT法）の研究」をネット上で発表します

第28回品質工学研究発表大会（RQES2020S）が開催中止となった為、ポスター発表する予定だった資料を画像に変換し、ネット上で研究成果を発表します。



----------------------
発表番号：【79】
発表日：2020年6月19日（火）→大会2日目です
発表形式：【ポスター発表】
論文表題：『非線形成分を考慮したMT法（2次元非線形MT法）の研究』
発表者名：増田雪也
詳細論文：8ページ版の詳細論文（PDFファイル、またはPDFファイル）
----------------------

※多次元非線形MT法（RQES2021Sにて発表）はこちら



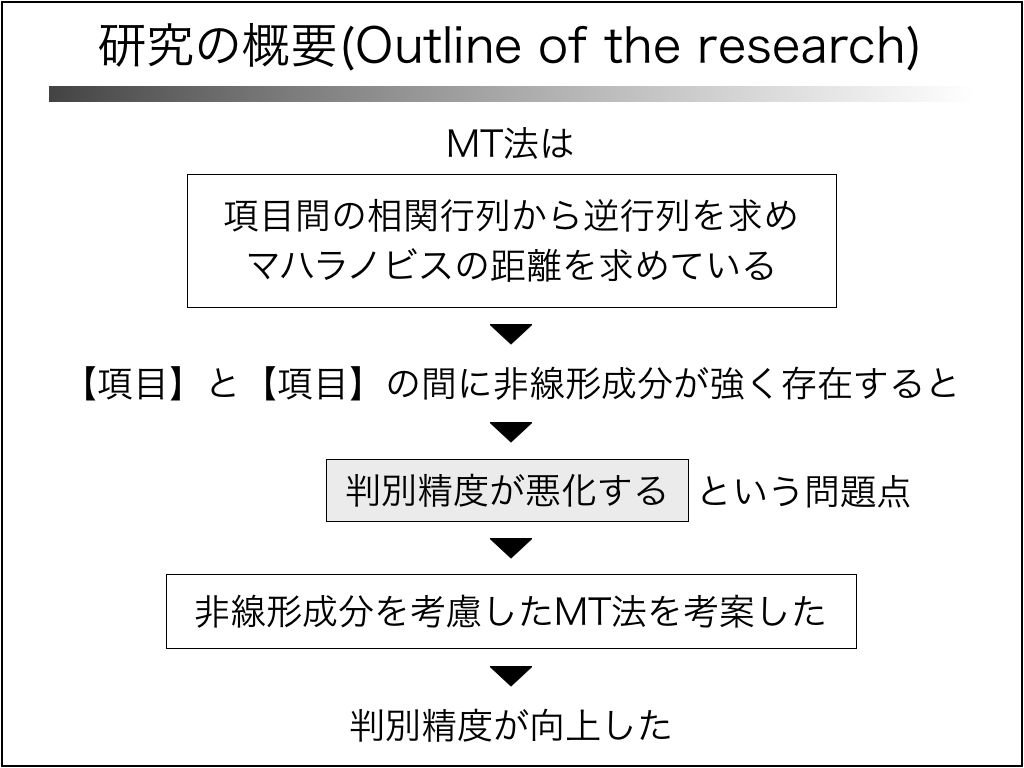
研究の概要を述べます。
MT法は、項目間の相関行列から逆行列を求め、マハラノビスの距離を求めています。
しかし、
【項目】と【項目】の間に非線形成分が強く存在すると、「判別精度が悪化する」という問題点があります。
そこで本研究では、
非線形成分を考慮したMT法を考案しました。
その結果、判別精度が向上しました。
----------------------

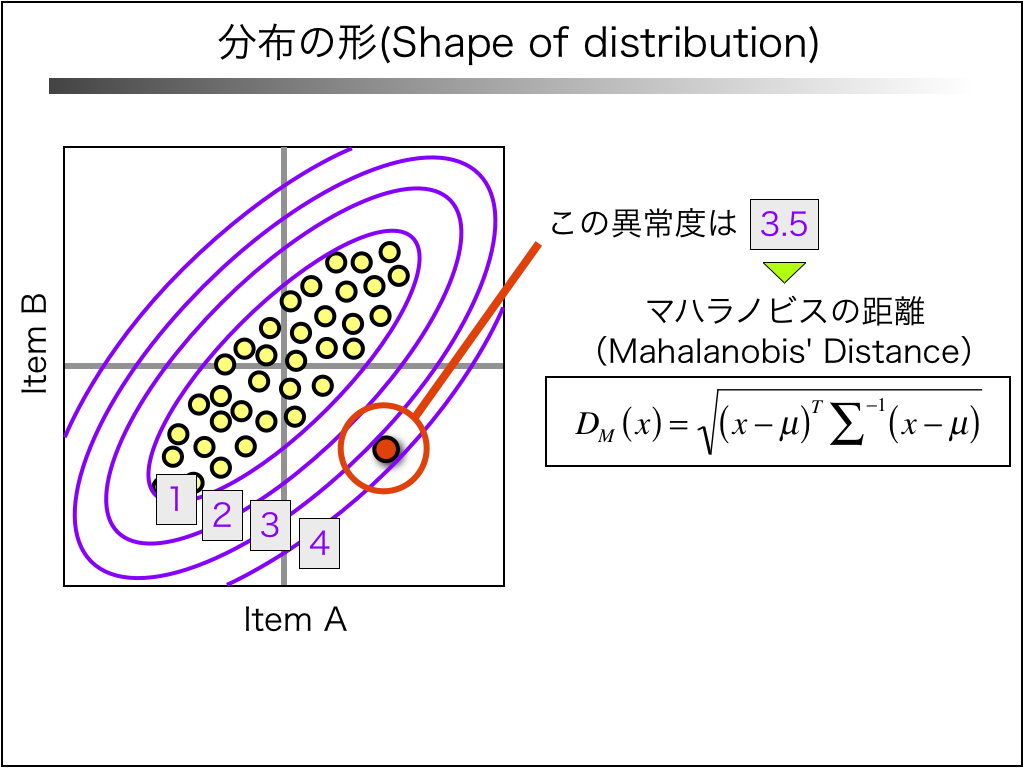
例えば、項目Aと項目Bがこのような分布をしていたとします。
すると、赤丸で示したデータの異常度は「3.5」となります。
これがマハラノビスの距離（以下、MD値と呼称する）です。
----------------------

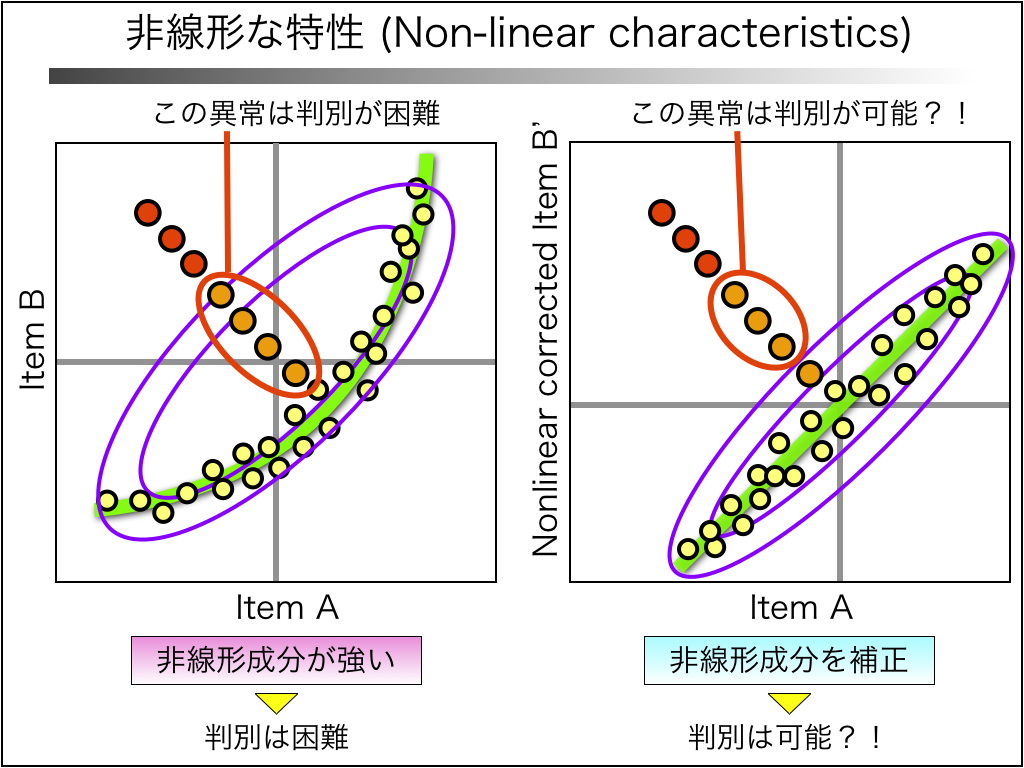
正常品（黄丸）において、項目Aと項目Bの間に非線形成分が存在すると、左の図のような分布となります。
この場合、異常品（オレンジ丸＆赤丸）を精度良く判別できるか？
オレンジ丸の異常品は、正常品の分布内に入っているため、MD値が小さくなり、「正常品である」と誤判別されます。

もしも、この非線形成分を補正し、非線形成分を小さくすることができたとしたら、右の図のような分布となります。
すると、誤判別されていたオレンジ丸の異常品の内、3つは「異常品である」と正しく判別されるはずです。
----------------------

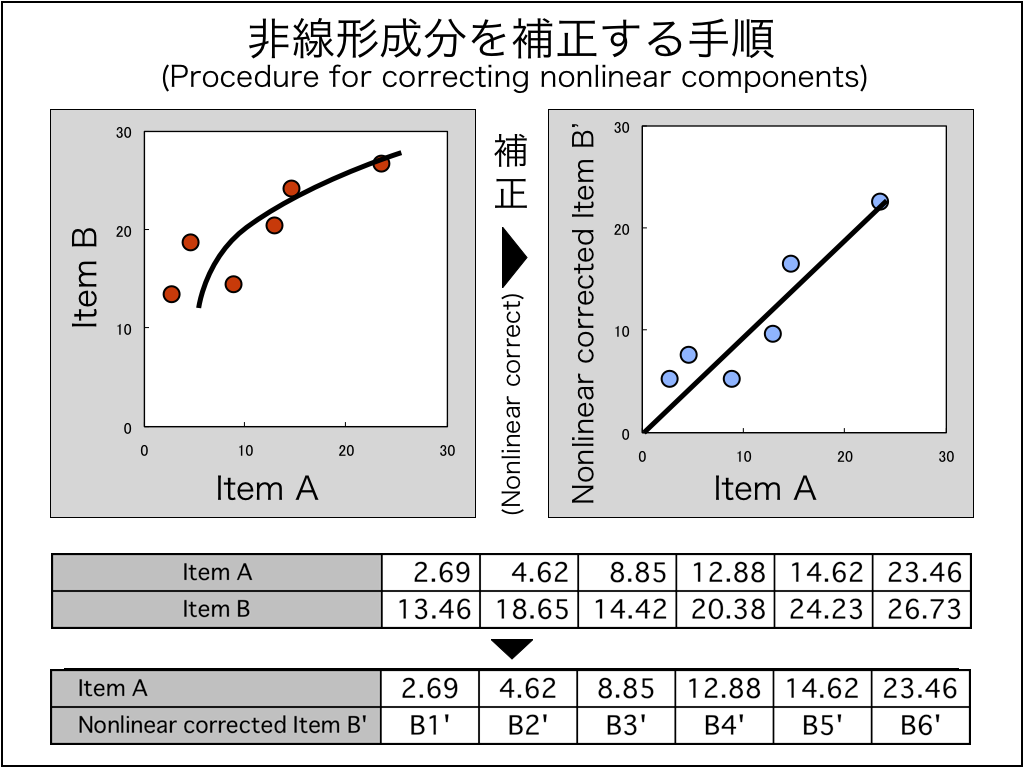
次に非線形成分を補正する方法について述べます。
左のグラフを右のグラフのように補正する場合で説明します。
補正するのは、グラフの縦軸です。
つまり、「項目値B」を補正し、「補正した項目値B’」とします。
----------------------

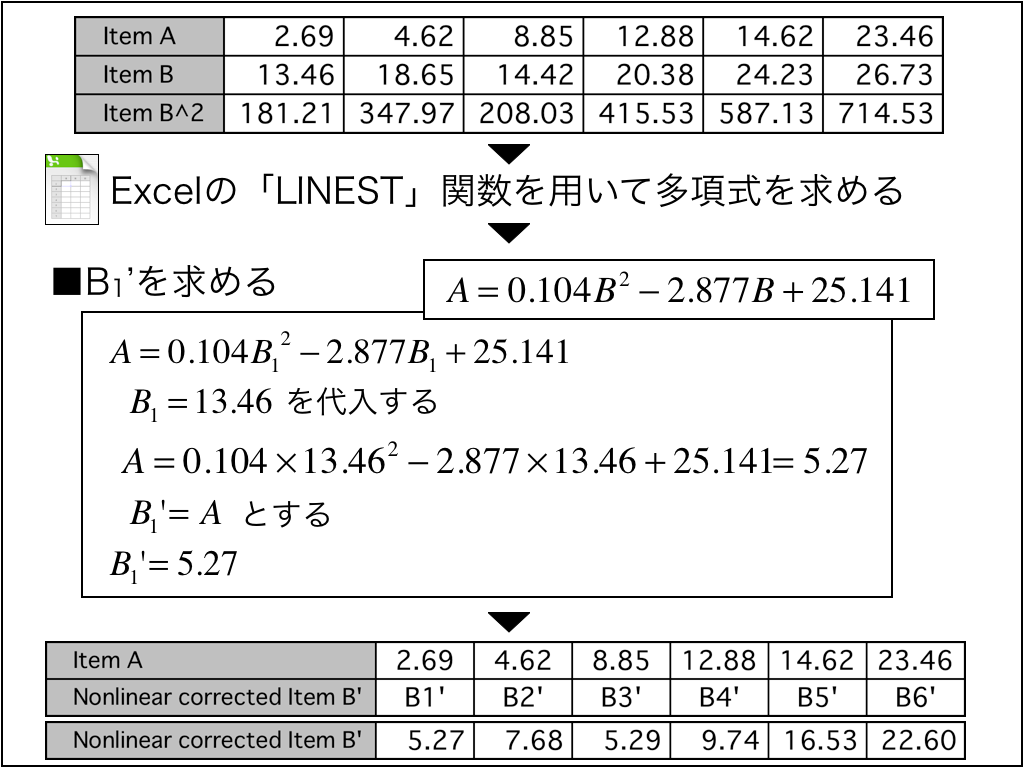
非線形成分を補正する方法の詳細説明をします。
2次の成分までを非線形補正しますので、上の表のように「項目値B^2」を求めます。
そして、エクセルの「LINEST」関数を用いて、「項目値A=・・・」の多項式を求めます。
この多項式に、「項目値B1=13.46」を代入すると、
A=5.27となります。
ここで、「補正した項目値B1’」について、B1’=Aとします。
よって、B1’=5.27となります。
このようにして補正したいくと、下の表のように「補正した項目値B’」が求まります。

なぜこんな方法で補正ができるのだろう？と疑問を感じる方も多いかと思いますが、
この方法だと、バラツキ成分はそのままで、非線形成分を補正することができます。
詳細につきましては、詳細論文にてグラフィカルな説明をしていますので、興味のある方はご参照下さい。

↓のエクセルファイルを使って、実際に上記の非線形補正の計算をすることができます。
----------------------
3.1 非線形補正の手順の計算.xls
----------------------
エクセルファイルをダウンロードし、ご参照下さい。
----------------------

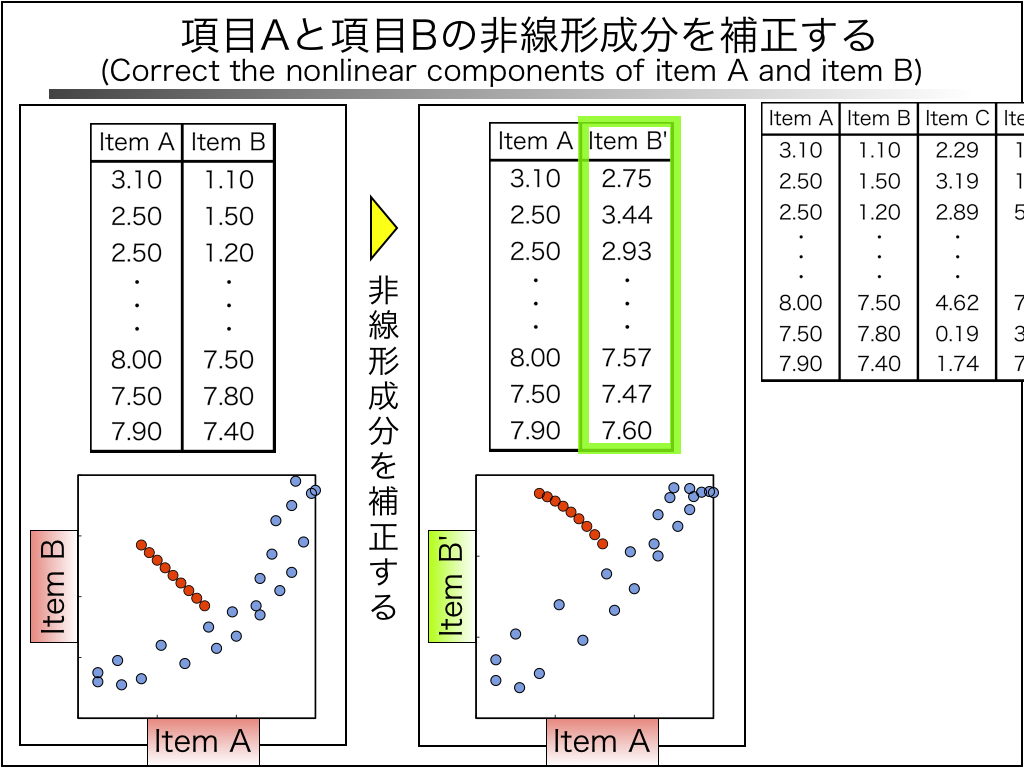
非線形MT法にてMD値を求める手順を説明します。
先ずは、先ほどの方法で項目Aと項目Bの非線形成分を補正します。
すると右のグラフのように非線形成分が補正され、直線に近い分布となります。
----------------------

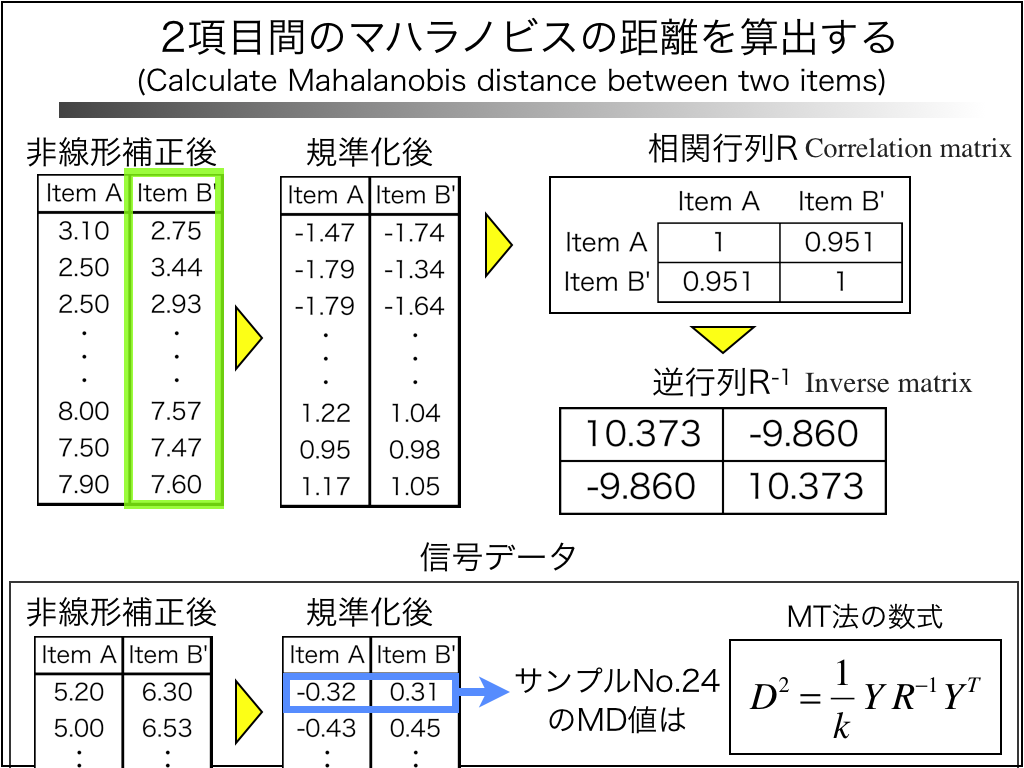
次に、非線形補正した項目Aと項目B'は、通常のMT法の手順と同じように計算していきます。
非線形補正後のデータを規準化（平均値を引き、標準偏差で割ります）し、項目Aと項目B'の相関行列を作り、その逆行列を求めます。
次に、求めたいサンプル（これも非線形補正をした後、規準化します）の値をMT法の数式に代入し、MD値を求めます。
----------------------

例えば、サンプルNo.24のMD値は、ご覧のように【2.033】となります。
この【2.033】は、「項目Aと項目B'」の組合せでのMD値です。
この解析において、項目は6つありますので、「項目Aと項目B'」のような2項目間の組合せは、全部で36通りあります。
そこで、全ての2項目間の組合せにおいて、同様に非線形補正を行い、MD値を求めます。
すると、サンプルNo.24のMD値は、36通りのMD値の集合体「MD値マトリクス」として表現できます。
この「MD値マトリクス」内のMD値の最大値を、そのサンプルの代表MD値とします。
つまり、サンプルNo.24では、最大値=2.033が代表MD値となります。
----------------------

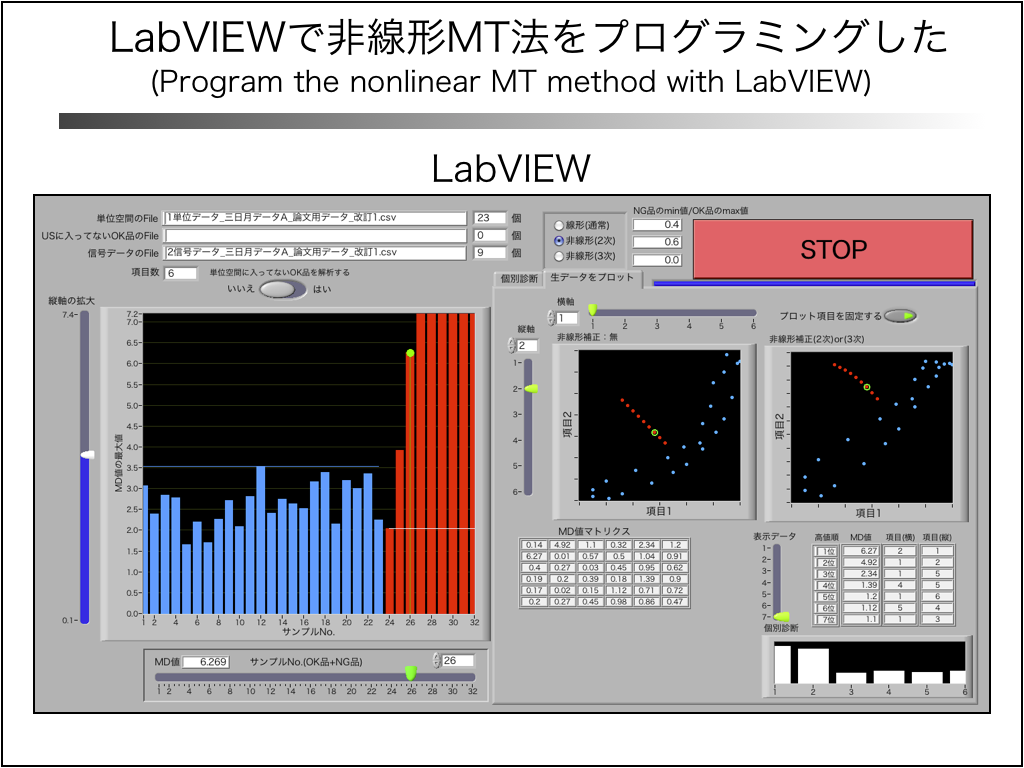
上記のような複雑な計算を汎用的に行うには、表計算ソフト「エクセル」では役不足です。
そこで、グラフィカルプログラミング言語「LabVIEW」を用いて、非線形MT法の計算をプログラミングしました。
----------------------

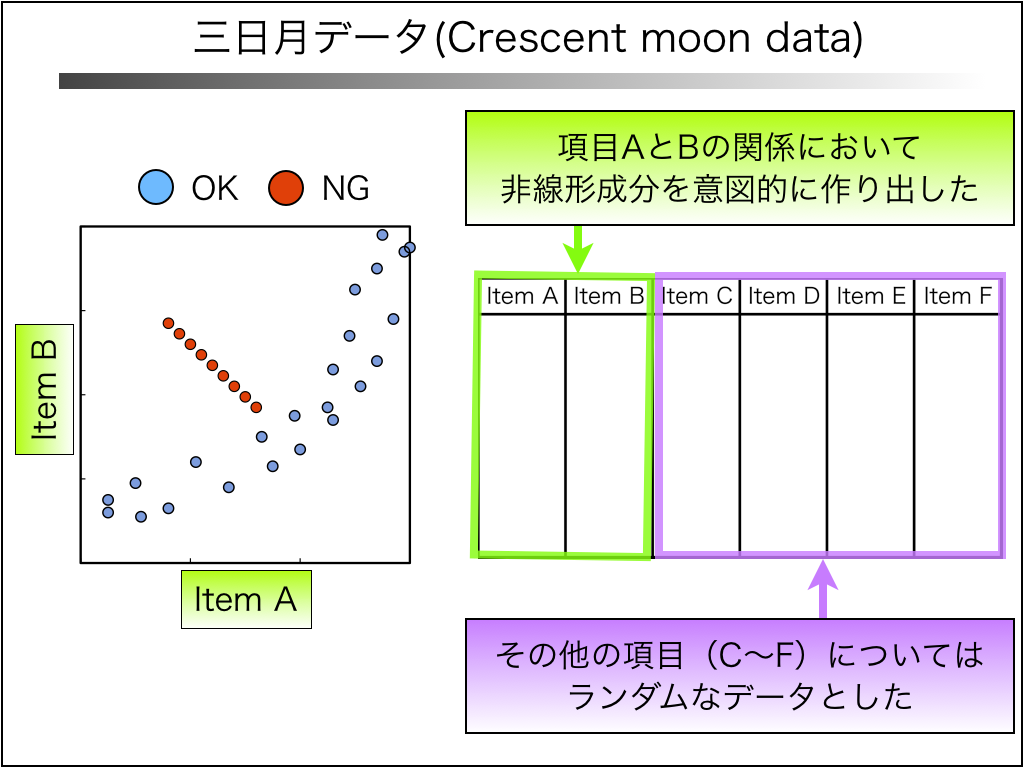
非線形MT法を用いて解析した事例を2つ紹介します。
1つ目は、先に紹介した「三日月データ」です。
このデータは、項目Aと項目Bの間に、図にあるような非線形成分を意図的に作り出しました。
その他の項目C〜Fいついては、ランダムなデータとしました。
----------------------

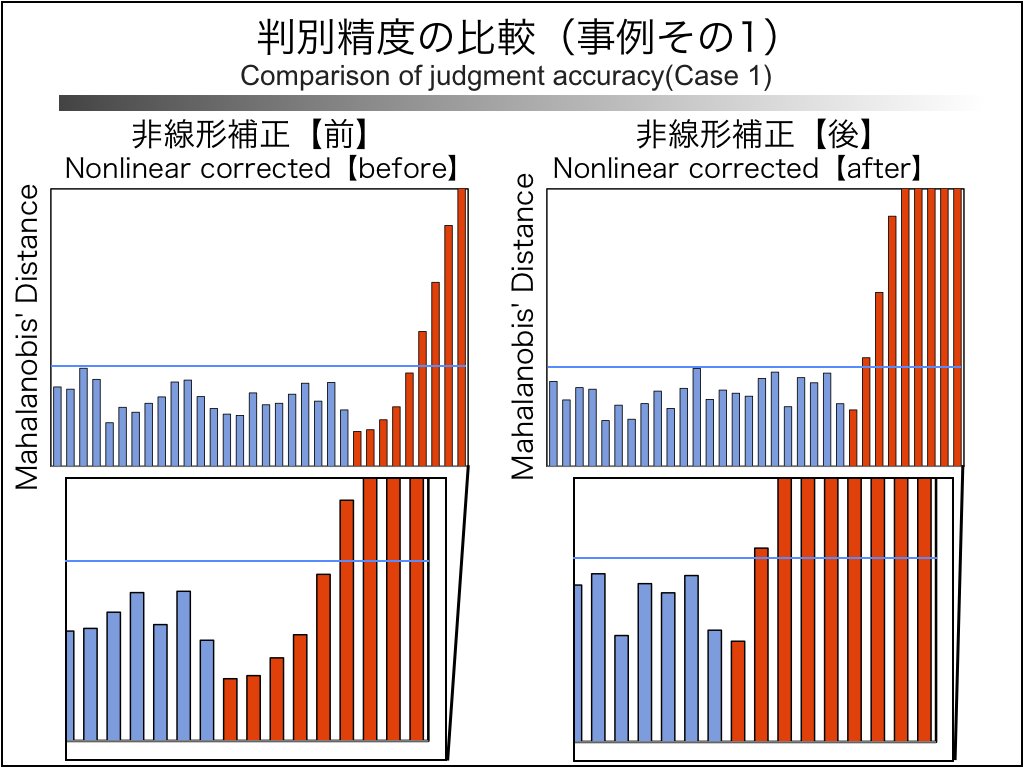
「三日月データ」の判別結果を示します。
左が非線形補正【前】、右が非線形補正【後】です。
青い棒グラフは正常品です。
赤い棒グラフは異常品です。
パッと見で分かるように、非線形補正【後】の方が判別精度が高くなっています。
----------------------

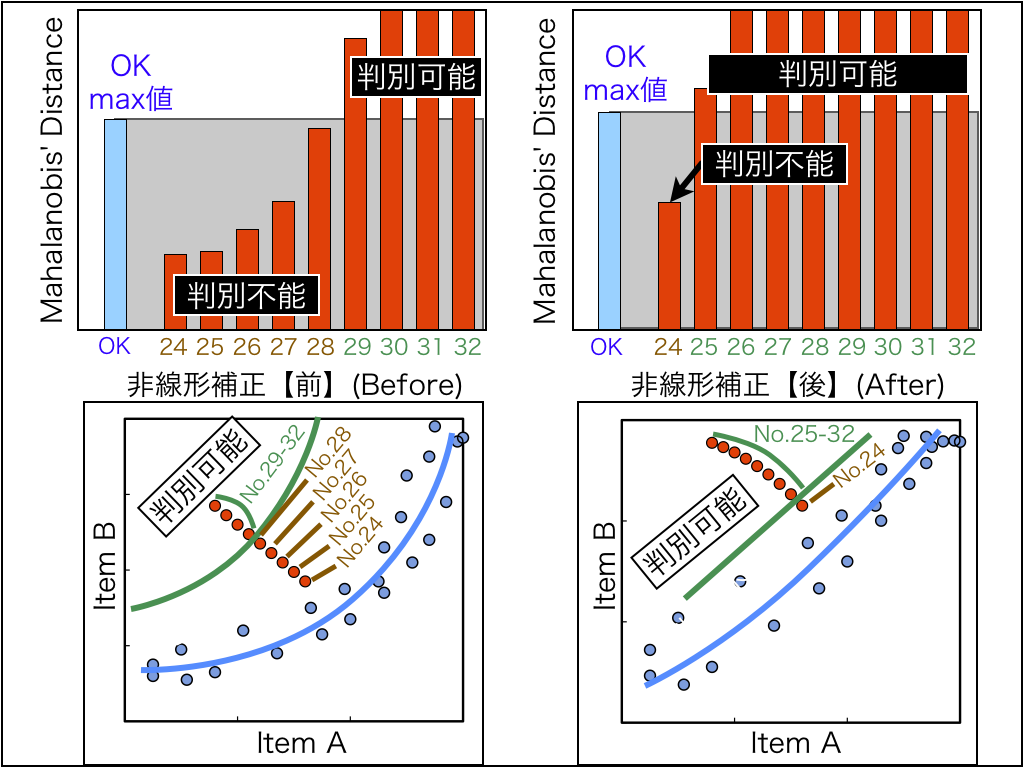
「三日月データ」の判別結果を詳細に見ていきます。
左の図から説明します。
非線形補正【前】では、異常品のNo.24〜28までは、正常品のMD値のmax値よりもMD値が低いため、「正常品である」と誤判別されています。
一方、右の非線形補正【後】では、異常品No.25〜32までは、正常品のMD値のmax値よりもMD値が高いため、「異常品である」と正しく判別されています。
----------------------

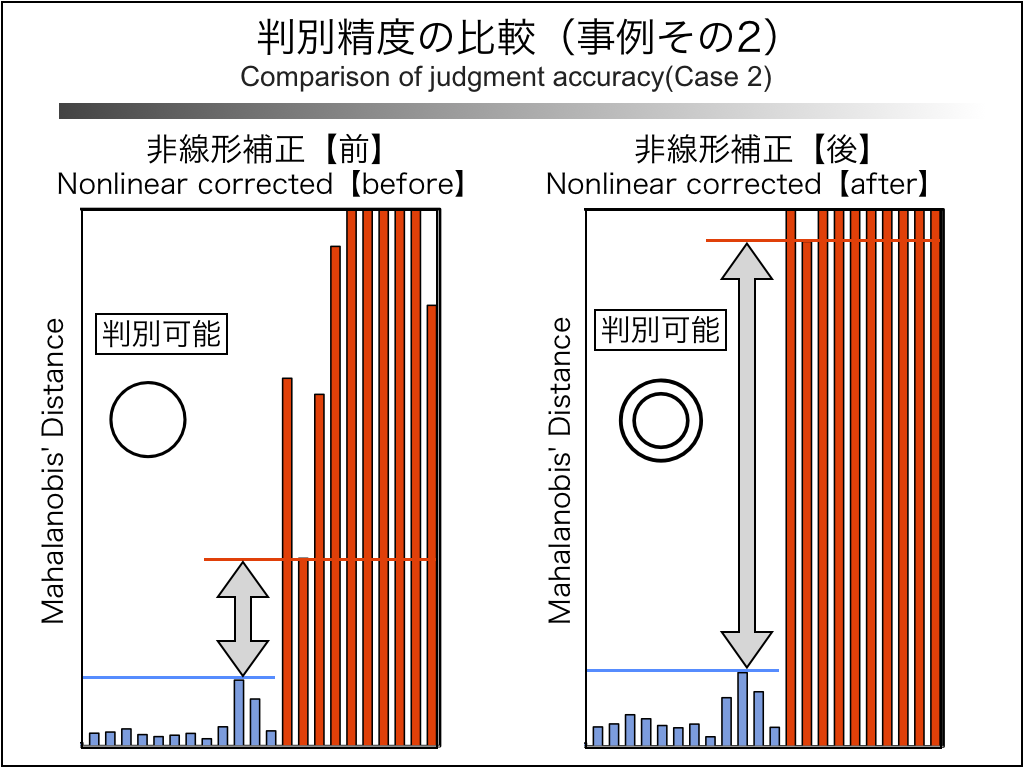
非線形MT法を用いて解析した事例の2つ目は、キーボードの打鍵時間のパターンから個人を判別した事例です。
キーボードから「ラーメン(ra-men)」と打鍵した際、Aさんが打鍵しのか、それ以外の人が打鍵したのかを判別した事例です。→詳細はこちら

この事例では、非線形補正の有無によらず、判別は可能となっています。
判別精度、つまり「正常品のMD値のmax値」と「異常品のMD値のmin値」の差に着目すると、左の非線形補正【前】よりも右の非線形補正【後】の方が、「正常品のMD値のmax値」と「異常品のMD値のmin値」の差が大きく開いており、判別精度が高いことが分かります。

以上、2つの事例で示したように、非線形補正することにより、判別精度が向上していることが分かります。
----------------------

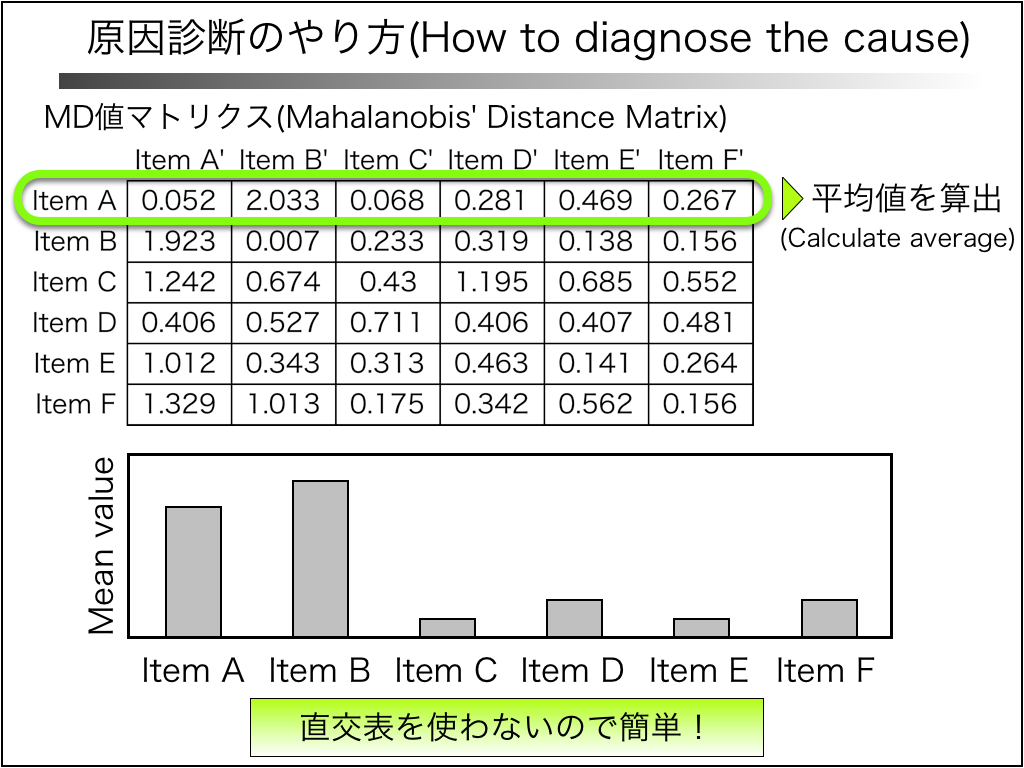
非線形MT法での原因診断（どの項目が効いているのか？）について述べます。
通常のMT法では、項目を「使う/使わない」を2水準系の直交表に割り付けて原因診断を行います。
非線形MT法では、MD値マトリクスの各項目の平均値を計算します。
とてもシンプルな方法なので、「計算が簡単」というメリットがあります。
----------------------

まとめです。
非線形成分を考慮したMT法（非線形MT法）を適用した結果、判別精度を向上させることができました。

より詳細な資料をご希望の方は、8ページ版の詳細論文（PDFファイル、またはPDFファイル）をご覧下さい。
----------------------

2020年度の研究発表大会（RQES2020S）が中止となった為、
研究成果を皆様に早く知っていただきたく、ネット上にて研究成果を発表しました。
しかしながら、本来の学会発表の目的である「研究内容をディスカッションする」という面においては、ネットでは難しいのが現状です。
そこで、2021年度の研究発表大会（RQES2021S）に再度エントリーする予定です。
※後記（2020/12/19）：「2次元非線形MT法」を更に発展させた「多次元非線形MT法」として、RQES2021Sにエントリーしました。